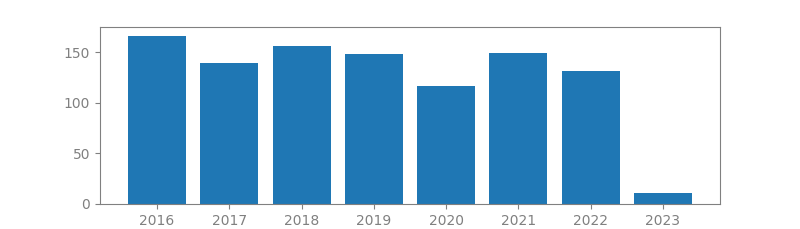
19 Most Cited Papers In Signal Processing
Signal Processing is a sub-field in the electrical engineering. It is growing rapidly due to the advance in the processing power of computers and Integrated Circuits (ICs), as well as mathematical theory of this field. In signal processing we manipulate and analysis of signals. The signal itself can be either analog or digital (sampled and quantized). Signal processing has many applications, for example, filtering electrical signals to remove unwanted noise, separating mixed signals from each other. An practical example is the noise cancelling headphones that many of us know and use. Today signal processing has applications in communications, control, biomedical engineering, image and video processing, economic forecasting, radar, sonar, geophysical exploration, and consumer electronics.
To come up with this list, we have used Google Scholar. In there we have done some extensive search and found the robotics most cited papers. Usually the more a paper is cited the more impact and importance it has. What we see in this blog post is a list of the 19 most cited papers in Signal Processing. For each paper, we include its authors, number of citations, publication year and location, as well as a summary. We have also ploted the citation trend for each paper that shows if the paper popularity has grown or declined over time.
1. ROBUST UNCERTAINTY PRINCIPLES: EXACT SIGNAL RECONSTRUCTION FROM HIGHLY INCOMPLETE FREQUENCY INFORMATION
Authors: Emmanuel J Candès, Justin Romberg, Terence Tao
Published in: IEEE Transactions on information theory, 2006
Number of citations: 18,771
Summary: This paper considers the model problem of reconstructing an object from incomplete frequency samples. Consider a discrete-time signal  and a randomly chosen set of frequencies
and a randomly chosen set of frequencies  of mean size
of mean size 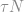 . Is it possible to reconstruct f from the partial knowledge of its Fourier coefficients on the set
. Is it possible to reconstruct f from the partial knowledge of its Fourier coefficients on the set  ? A typical result of this paper is as follows: for each M > 0 Suppose that f obeys
? A typical result of this paper is as follows: for each M > 0 Suppose that f obeys 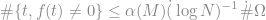 , then with probability at least
, then with probability at least 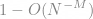 , f can be reconstructed exactly as the solution to the
, f can be reconstructed exactly as the solution to the 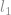 minimization problem
minimization problem
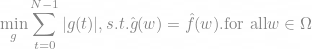
2. INDEPENDENT COMPONENT ANALYSIS, A NEW CONCEPT?
Authors: Pierre Comon
Published in: Signal processing, 1994
Number of citations: 11,772
Summary: The independent component analysis (ICA) of a random vector consists of searching for a linear transformation that minimizes the statistical dependence between its components. In order to define suitable search criteria, the expansion of mutual information is utilized as a function of cumulants of increasing orders. An efficient algorithm is proposed, which allows the computation of the ICA of a data matrix within a polynomial time. The concept of ICA may actually be seen as an extension of the principal component analysis (PCA), which can only impose independence up to the second order and, consequently, defines directions that are orthogonal. Potential applications of ICA include data analysis and compression, Bayesian detection, localization of sources, and blind identification and deconvolution.
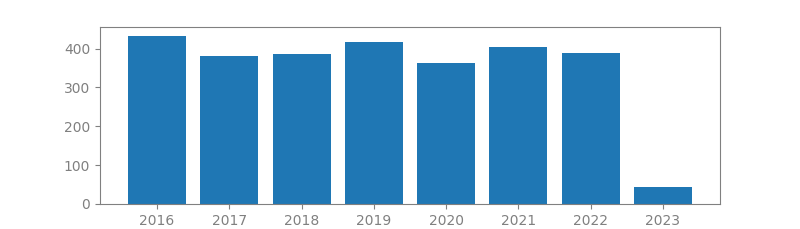
3. AN INTRODUCTION TO COMPRESSIVE SAMPLING
Authors: Emmanuel J Candès, Michael B Wakin
Published in: Signal Processing Magazine, IEEE, 2008
Number of citations: 11,642
Summary: Conventional approaches to sampling signals or images follow Shannon’s theorem: the sampling rate must be at least twice the maximum frequency present in the signal (Nyquist rate). In the field of data conversion, standard analog-to-digital converter (ADC) technology implements the usual quantized Shannon representation - the signal is uniformly sampled at or above the Nyquist rate. This article surveys the theory of compressive sampling, also known as compressed sensing or CS, a novel sensing/sampling paradigm that goes against the common wisdom in data acquisition. CS theory asserts that one can recover certain signals and images from far fewer samples or measurements than traditional methods use.
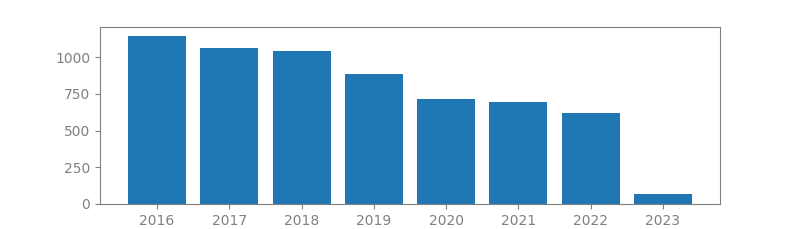
4. K-SVD: AN ALGORITHM FOR DESIGNING OVERCOMPLETE DICTIONARIES FOR SPARSE REPRESENTATION
Authors: Michal Aharon, Michael Elad, Alfred Bruckstein
Published in: IEEE Transactions on signal processing, 2006
Number of citations: 11,304
Summary: In recent years there has been a growing interest in the study of sparse representation of signals. Using an overcomplete dictionary that contains prototype signal-atoms, signals are described by sparse linear combinations of these atoms. Applications that use sparse representation are many and include compression, regularization in inverse problems, feature extraction, and more. Recent activity in this field has concentrated mainly on the study of pursuit algorithms that decompose signals with respect to a given dictionary. Designing dictionaries to better fit the above model can be done by either selecting one from a prespecified set of linear transforms or adapting the dictionary to a set of training signals. Both of these techniques have been considered, but this topic is largely still open. In this paper we propose a novel algorithm for adapting dictionaries in order to achieve sparse signal representations. Given a set…
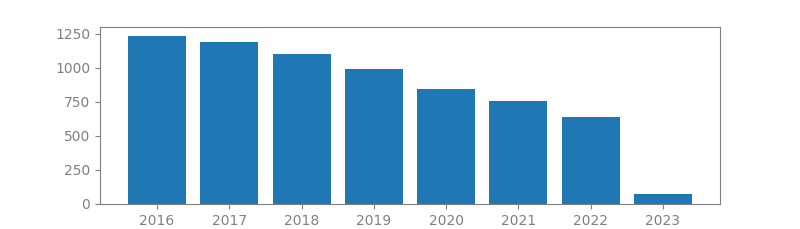
5. AN ALGORITHM FOR VECTOR QUANTIZER DESIGN
Authors: Yoseph Linde, Andres Buzo, Robert Gray
Published in: IEEE Transactions on communications, 1980
Number of citations: 10,996
Summary: An efficient and intuitive algorithm is presented for the design of vector quantizers based either on a known probabilistic model or on a long training sequence of data. The basic properties of the algorithm are discussed and demonstrated by examples. Quite general distortion measures and long blocklengths are allowed, as exemplified by the design of parameter vector quantizers of ten-dimensional vectors arising in Linear Predictive Coded (LPC) speech compression with a complicated distortion measure arising in LPC analysis that does not depend only on the error vector.
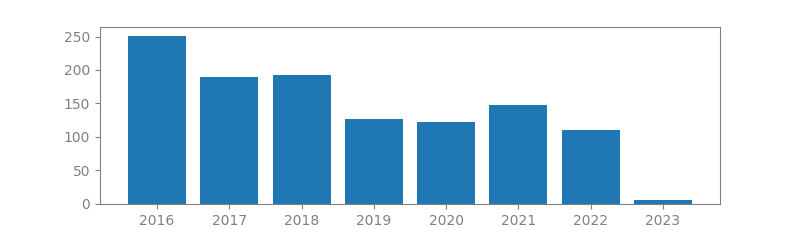
6. THE UNSCENTED KALMAN FILTER FOR NONLINEAR ESTIMATION
Authors: Eric A Wan, Rudolph Van Der Merwe
Published in: Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (Cat. No. 00EX373), 2000
Number of citations: 5,534
Summary: This paper points out the flaws in using the extended Kalman filter (EKE) and introduces an improvement, the unscented Kalman filter (UKF), proposed by Julier and Uhlman (1997). A central and vital operation performed in the Kalman filter is the propagation of a Gaussian random variable (GRV) through the system dynamics. In the EKF the state distribution is approximated by a GRV, which is then propagated analytically through the first-order linearization of the nonlinear system. This can introduce large errors in the true posterior mean and covariance of the transformed GRV, which may lead to sub-optimal performance and sometimes divergence of the filter. The UKF addresses this problem by using a deterministic sampling approach. The state distribution is again approximated by a GRV, but is now represented using a minimal set of carefully chosen sample points. These sample points completely capture the…
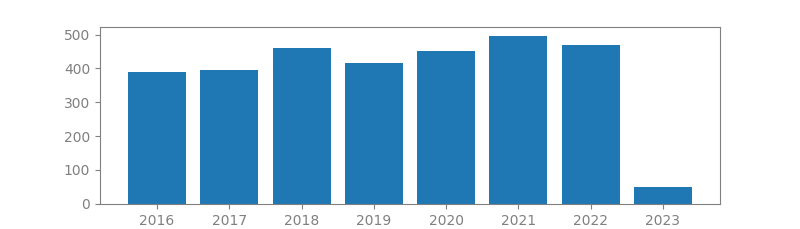
7. BEAMFORMING: A VERSATILE APPROACH TO SPATIAL FILTERING
Authors: Barry D Van Veen, Kevin M Buckley
Published in: IEEE assp magazine, 1988
Number of citations: 5,500
Summary: A beamformer is a processor used in conjunction with an array of sensors to provide a versatile form of spatial filtering. The sensor array collects spatial samples of propagating wave fields, which are processed by the beamformer. The objective is to estimate the signal arriving from a desired direction in the presence of noise and interfering signals. A beamformer performs spatial filtering to separate signals that have overlapping frequency content but originate from different spatial locations. In this paper an overview of beamforming from a signal-processing perspective is provided, with an emphasis on recent research. Data-independent, statistically optimum, adaptive, and partially adaptive beamforming are discussed. Basic notation, terminology, and concepts are included. Several beamformer implementations are briefly described.
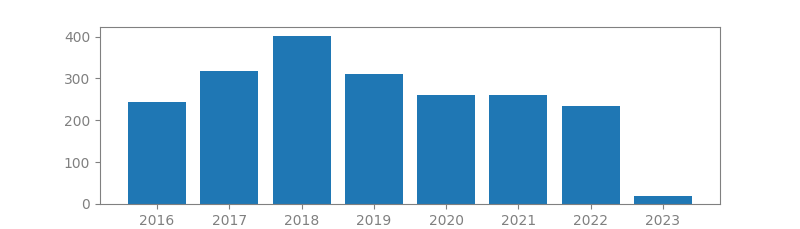
8. TWO DECADES OF ARRAY SIGNAL PROCESSING RESEARCH: THE PARAMETRIC APPROACH
Authors: Hamid Krim, Mats Viberg
Published in: IEEE signal processing magazine, 1996
Number of citations: 5,453
Summary: The quintessential goal of sensor array signal processing is the estimation of parameters by fusing temporal and spatial information, captured via sampling a wavefield with a set of judiciously placed antenna sensors. The wavefield is assumed to be generated by a finite number of emitters, and contains information about signal parameters characterizing the emitters. A review of the area of array processing is given. The focus is on parameter estimation methods, and many relevant problems are only briefly mentioned. We emphasize the relatively more recent subspace-based methods in relation to beamforming. The article consists of background material and of the basic problem formulation. Then we introduce spectral-based algorithmic solutions to the signal parameter estimation problem. We contrast these suboptimal solutions to parametric methods. Techniques derived from maximum likelihood principles as…
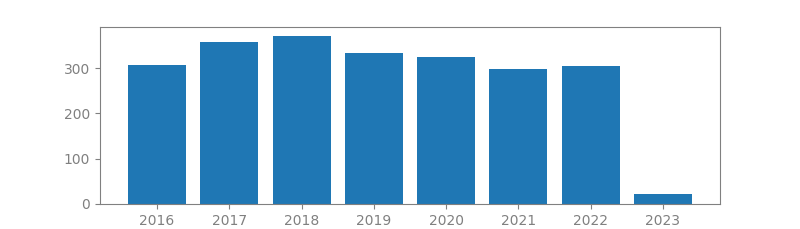
9. ENHANCING SPARSITY BY REWEIGHTED l1 MINIMIZATION
Authors: Emmanuel J Candes, Michael B Wakin, Stephen P Boyd
Published in: Journal of Fourier analysis and applications, 2008
Number of citations: 5,262
Summary: It is now well understood that (1) it is possible to reconstruct sparse signals exactly from what appear to be highly incomplete sets of linear measurements and (2)that this can be done by constrained l1 minimization. In this paper, we study a novel method for sparse signal recovery that in many situations outperforms l1 minimization in the sense that substantially fewer measurements are needed for exact recovery. The algorithm consists of solving a sequence of weighted l1-minimization problems where the weights used for the next iteration are computed from the value of the current solution. We present a series of experiments demonstrating the remarkable performance and broad applicability of this algorithm in the areas of sparse signal recovery, statistical estimation, error correction and image processing. Interestingly, superior gains are also achieved when our…
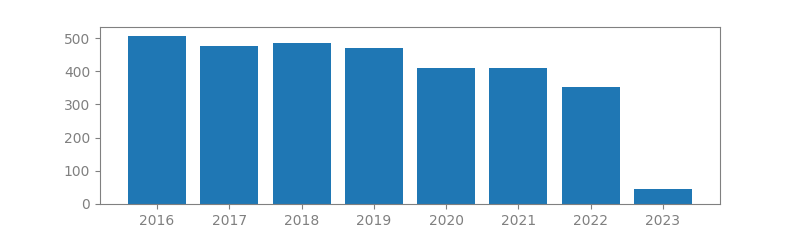
10. VECTOR QUANTIZATION
Authors: Robert Gray
Published in: IEEE Assp Magazine, 1984
Number of citations: 4,520
Summary: A vector quantizer is a system for mapping a sequence of continuous or discrete vectors into a digital sequence suitable for communication over or storage in a digital channel. The goal of such a system is data compression: to reduce the bit rate so as to minimize communication channel capacity or digital storage memory requirements while maintaining the necessary fidelity of the data. The mapping for each vector may or may not have memory in the sense of depending on past actions of the coder, just as in well established scalar techniques such as PCM, which has no memory, and predictive quantization, which does. Even though information theory implies that one can always obtain better performance by coding vectors instead of scalars, scalar quantizers have remained by far the most common data compression system because of their simplicity and good performance when the communication rate is…
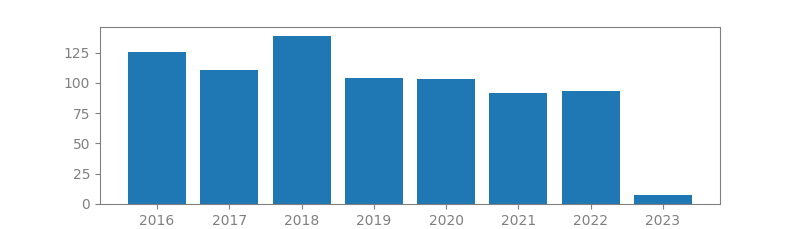
11. COMPRESSIVE SAMPLING
Authors: Emmanuel J Candès
Published in: Proceedings of the international congress of mathematicians, 2006
Number of citations: 4,501
Summary: Conventional wisdom and common practice in acquisition and reconstruction of images from frequency data follow the basic principle of the Nyquist density sampling theory. This principle states that to reconstruct an image, the number of Fourier samples we need to acquire must match the desired resolution of the image, ie the number of pixels in the image. This paper surveys an emerging theory which goes by the name of “compressive sampling” or “compressed sensing,” and which says that this conventional wisdom is inaccurate. Perhaps surprisingly, it is possible to reconstruct images or signals of scientific interest accurately and sometimes even exactly from a number of samples which is far smaller than the desired resolution of the image/signal, eg the number of pixels in the image. It is believed that compressive sampling has far reaching implications. For example, it suggests the possibility of new data acquisition protocols that translate analog information into digital form with fewer sensors than what was considered necessary. This new sampling theory may come to underlie procedures for sampling and compressing data simultaneously. In this short survey, we provide some of the key mathematical insights underlying this new theory, and explain some of the interactions between compressive sampling and other fields such as statistics, information theory, coding theory, and theoretical computer science.
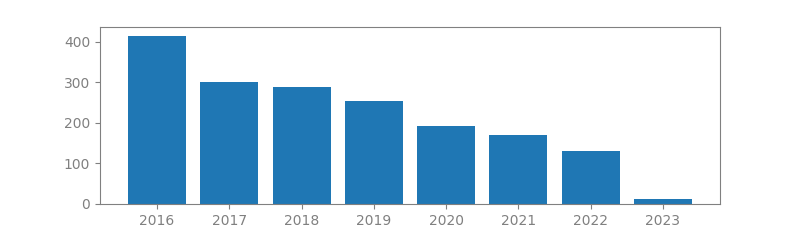
12. WAVELETS AND SIGNAL PROCESSING
Authors: Olivier Rioul, Martin Vetterli
Published in: IEEE signal processing magazine, 1991
Number of citations: 4,085
Summary: Wavelet theory provides a unified framework for a number of techniques which had been developed independently for various signal processing applications. For example, multiresolution signal processing, used in computer vision; subband coding, developed for speech and image compression; and wavelet series expansions, developed in applied mathematics, have been recently recognized as different views of a single theory. In this paper a simple, nonrigorous, synthetic view of wavelet theory is presented for both review and tutorial purposes. The discussion includes nonstationary signal analysis, scale versus frequency, wavelet analysis and synthesis, scalograms, wavelet frames and orthonormal bases, the discrete-time case, and applications of wavelets in signal processing. The main definitions and properties of wavelet transforms are covered, and connections among the various fields where results have been developed are shown.
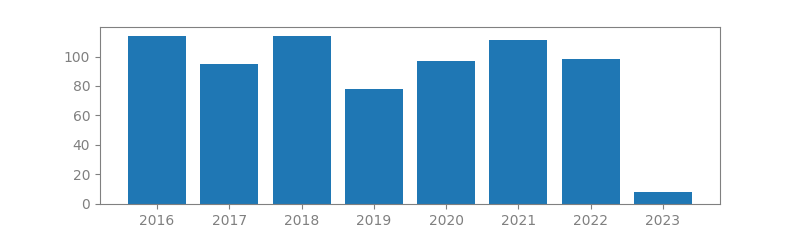
13. GRADIENT PROJECTION FOR SPARSE RECONSTRUCTION: APPLICATION TO COMPRESSED SENSING AND OTHER INVERSE PROBLEMS
Authors: Mário AT Figueiredo, Robert D Nowak, Stephen J Wright
Published in: Selected Topics in Signal Processing, IEEE Journal of, 2007
Number of citations: 4,111
Summary: Many problems in signal processing and statistical inference involve finding sparse solutions to under-determined, or ill-conditioned, linear systems of equations. A standard approach consists in minimizing an objective function which includes a quadratic (squared ) error term combined with a sparseness-inducing regularization term. Basis pursuit, the least absolute shrinkage and selection operator (LASSO), wavelet-based deconvolution, and compressed sensing are a few well-known examples of this approach. This paper proposes gradient projection (GP) algorithms for the bound-constrained quadratic programming (BCQP) formulation of these problems. We test variants of this approach that select the line search parameters in different ways, including techniques based on the Barzilai-Borwein method. Computational experiments show that these GP approaches perform well in a wide range of applications…
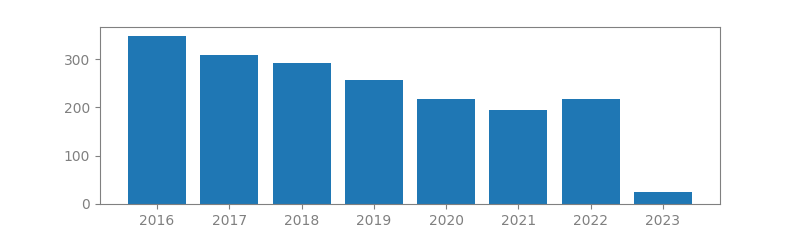
14. BLIND BEAMFORMING FOR NON-GAUSSIAN SIGNALS
Authors: Jean-François Cardoso, Antoine Souloumiac
Published in: IEE proceedings F (radar and signal processing), 1993
Number of citations: 3,893
Summary: The paper considers an application of blind identification to beamforming. The key point is to use estimates of directional vectors rather than resort to their hypothesised value. By using estimates of the directional vectors obtained via blind identification, i.e. without knowing the array manifold, beamforming is made robust with respect to array deformations, distortion of the wave front, pointing errors etc., so that neither array calibration nor physical modelling is necessary. Rather suprisingly, ‘blind beamformers’ may outperform ‘informed beamformers’ in a plausible range of parameters, even when the array is perfectly known to the informed beamformer. The key assumption on which blind identification relies is the statistical independence of the sources, which is exploited using fourth-order cumulants. A computationally efficient technique is presented for the blind estimation of directional vectors, based on joint …
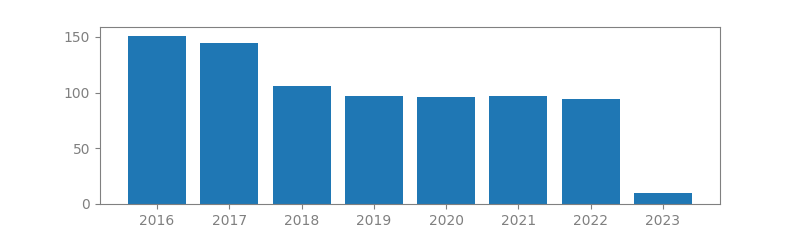
15. ZERO-FORCING METHODS FOR DOWNLINK SPATIAL MULTIPLEXING IN MULTIUSER MIMO CHANNELS
Authors: Quentin H Spencer, A Lee Swindlehurst, Martin Haardt
Published in: IEEE transactions on signal processing, 2004
Number of citations: 3,846
Summary: The use of space-division multiple access (SDMA) in the downlink of a multiuser multiple-input, multiple-output (MIMO) wireless communications network can provide a substantial gain in system throughput. The challenge in such multiuser systems is designing transmit vectors while considering the co-channel interference of other users. Typical optimization problems of interest include the capacity problem - maximizing the sum information rate subject to a power constraint-or the power control problem-minimizing transmitted power such that a certain quality-of-service metric for each user is met. Neither of these problems possess closed-form solutions for the general multiuser MIMO channel, but the imposition of certain constraints can lead to closed-form solutions. This paper presents two such constrained solutions. The first, referred to as “block-diagonalization,” is a generalization of channel inversion when there…
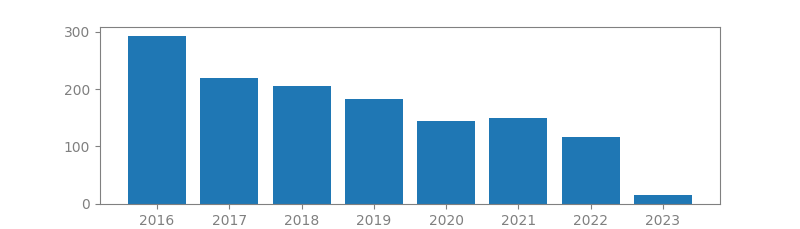
16. BLIND SEPARATION OF SOURCES, PART I: AN ADAPTIVE ALGORITHM BASED ON NEUROMIMETIC ARCHITECTURE
Authors: Christian Jutten, Jeanny Herault
Published in: Signal processing, 1991
Number of citations: 3,793
Summary: The separation of independent sources from an array of sensors is a classical but difficult problem in signal processing. Based on some biological observations, an adaptive algorithm is proposed to separate simultaneously all the unknown independent sources. The adaptive rule, which constitutes an independence test using non-linear functions, is the main original point of this blind identification procedure. Moreover, a new concept, that of INdependent Components Analysis (INCA), more powerful than the classical Principal Components Analysis (in decision tasks) emerges from this work.
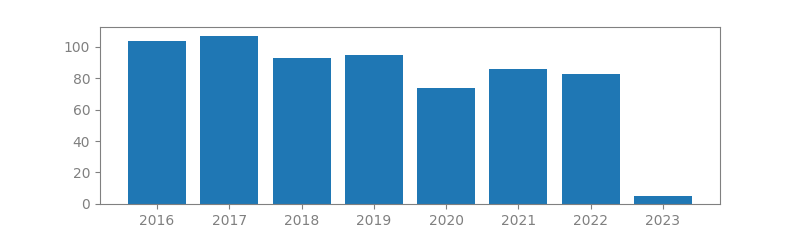
17. SINGLE-PIXEL IMAGING VIA COMPRESSIVE SAMPLING
Authors: Marco F Duarte, Mark A Davenport, Dharmpal Takhar, Jason N Laska, Ting Sun, Kevin F Kelly, Richard G Baraniuk
Published in: IEEE Signal Processing Magazine, 2008
Number of citations: 3,781
Summary: The authors present a new approach to building simpler, smaller, and cheaper digital cameras that can operate efficiently across a broader spectral range than conventional silicon-based cameras. The approach fuses a new camera architecture based on a digital micromirror device with the new mathematical theory and algorithms of compressive sampling.
18. A SURVEY OF DYNAMIC SPECTRUM ACCESS
Authors: Qing Zhao, Brian M Sadler
Published in: IEEE signal processing magazine, 2007
Number of citations: 3,586
Summary: Compounding the confusion is the use of the broad term cognitive radio as a synonym for dynamic spectrum access. As an initial attempt at unifying the terminology, the taxonomy of dynamic spectrum access is provided. In this article, an overview of challenges and recent developments in both technological and regulatory aspects of opportunistic spectrum access (OSA). The three basic components of OSA are discussed. Spectrum opportunity identification is crucial to OSA in order to achieve nonintrusive communication. The basic functions of the opportunity identification module are identified
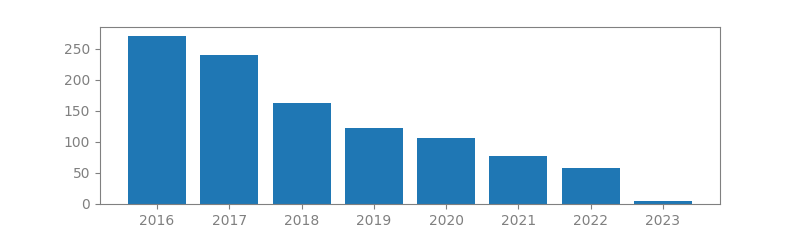
19. A BLIND SOURCE SEPARATION TECHNIQUE USING SECOND-ORDER STATISTICS
Authors: Adel Belouchrani, Karim Abed-Meraim, J-F Cardoso, Eric Moulines
Published in: IEEE Transactions on signal processing, 1997
Number of citations: 3,502
Summary: Separation of sources consists of recovering a set of signals of which only instantaneous linear mixtures are observed. In many situations, no a priori information on the mixing matrix is available: The linear mixture should be “blindly” processed. This typically occurs in narrowband array processing applications when the array manifold is unknown or distorted. This paper introduces a new source separation technique exploiting the time coherence of the source signals. In contrast with other previously reported techniques, the proposed approach relies only on stationary second-order statistics that are based on a joint diagonalization of a set of covariance matrices. Asymptotic performance analysis of this method is carried out; some numerical simulations are provided to illustrate the effectiveness of the proposed method.